Polygones hyperboliques réguliers et ses translatés par Marcel Morales

Tous les polygones représentés sont réguliers, c.a.d. ses côtés sont de même longueur et ses angles de même mesure.
Le polygone de gauche est centré à l’origine. Celui du milieu est son translaté vers la gauche.
A droite on a construit un polygone régulier de coté plus grand, remarquez que plus le polygone
devient grand plus ses angles deviennent petits, ce qui s’explique par le
Théorème de Gauss-Bonnet : L’aire hyperbolique d’un triangle hyperbolique d’angles a,ß,g, est pi-(a+ß+g).
Pour un polygone hyperbolique P de n côtés soit G la somme de ses angles alors airehyp(P)= (n-2)pi-G.

/polygones-hyperboliques/triangle-1.JPG

/polygones-hyperboliques/triangle-2.JPG

/polygones-hyperboliques/triangle-3.JPG

/polygones-hyperboliques/carre-1.JPG

/polygones-hyperboliques/carre-2.JPG

/polygones-hyperboliques/carre-3.JPG
TRIANGLE
TRIANGLE TRIANGLE CARRE
 CARRE CARRE

/polygones-hyperboliques/pentagone-1.JPG

file:///polygones-hyperboliques/pentagone-2.JPG

file:///polygones-hyperboliques/pentagone-3.JPG

file:///polygones-hyperboliques/pentagonestar-1.JPG

file:///polygones-hyperboliques/hexagone-1.JPG

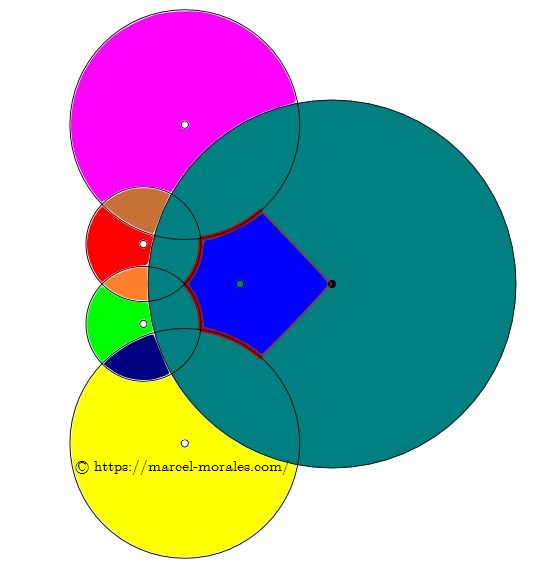
file:///polygones-hyperboliques/hexagone-2.JPG
PENTAGONE
 PENTAGONE PENTAGONE
 PENTAGONE STAR
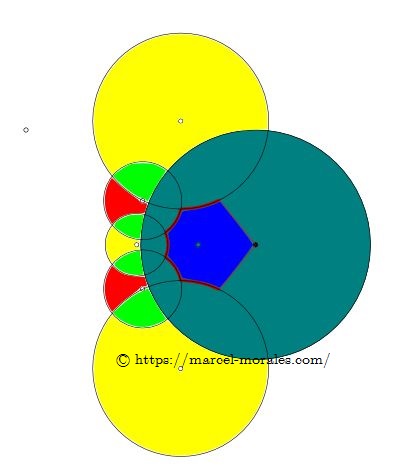
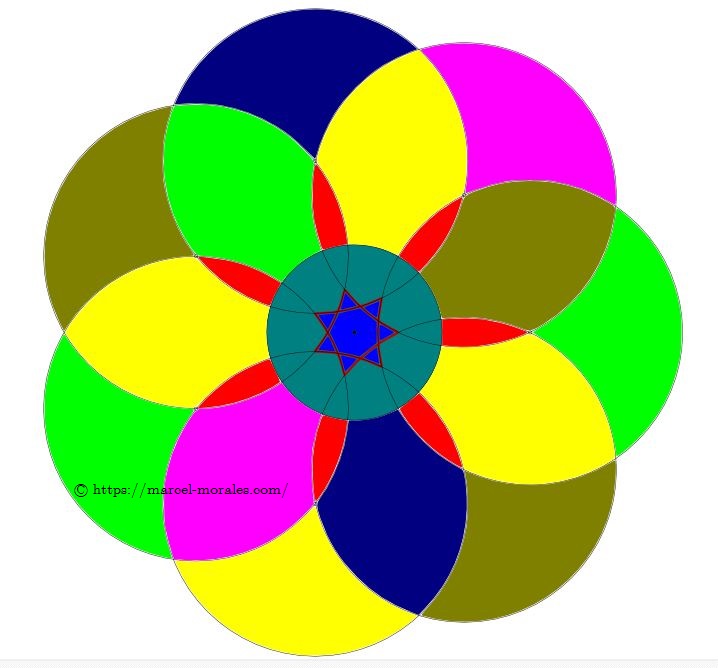
 HEXAGONE HEXAGONE

/polygones-hyperboliques/hexagone-3.JPG

/polygones-hyperboliques/heptagone-1.JPG

/polygones-hyperboliques/heptagone-2.JPG

/polygones-hyperboliques/heptagonestar-3.JPG

/polygones-hyperboliques/heptagonestar-4.JPG

/polygones-hyperboliques/eneagone-1.JPG
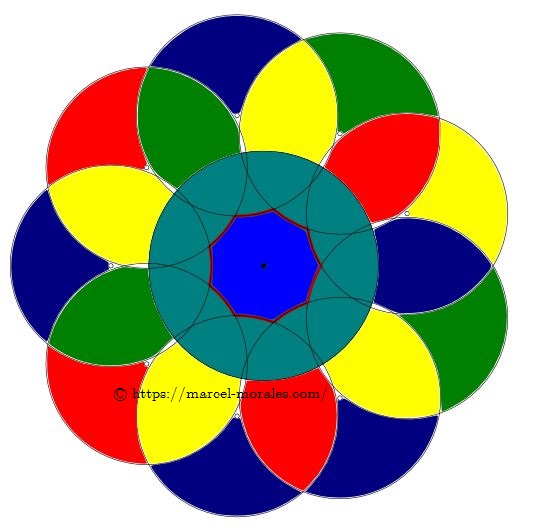
HEXAGONE HEPTAGONE HEPTAGONE HEPTAGONE STAR HEPTAGONE STAR ENEAGONE

/polygones-hyperboliques/eneagonestar-2.JPG

/polygones-hyperboliques/eneagonestar-3.JPG

/polygones-hyperboliques/endecagone-1.JPG

/polygones-hyperboliques/endecagonestar-2.JPG

/polygones-hyperboliques/decatrigonestar-2.JPG

/polygones-hyperboliques/decatrigonestar-3.JPG
ENEAGONE STAR ENEAGONE STAR ENDECAGONE ENDECAGONE STAR DECATRIGONE STAR DECATRIGONE STAR